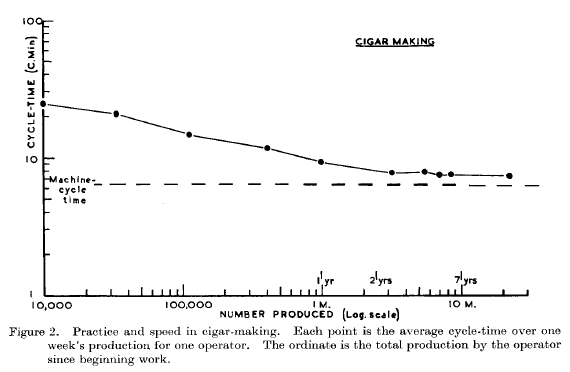
There’s a famous old data set on skill learning & expertise on workers rolling cigars that is used as an example of trying to understand the underlying skill learning rate (and therefore process). I was reminded of the data by Scott Grafton last week and thought I’d dig it up for the lab website. I found the article:
Crossman, E. R. F. W. A theory of the acquisition of speed-skill. Ergonomics 2, 153–166 (1959).
But it turns out our library subscription of the journal Ergonomics only goes back to 1997. I’ve put in a ILL request for the article and will update this with a learning curve picture when it arrives.
The data are sometimes used as part of a math-psych debate about whether skill learning produces an “exponential” shaped learning curve or a “power law” shaped learning curve. These are the mathematical forms of these curves:
Power: E(RT) = A + B * N^-β
Exponential: E(RT) = A + Be^-(α N)
E(RT) (expected value of RT at this point in training) is the data fit as a function of free parameters: A, B plus the learning rate parameters (beta for power, alpha for exponential). A reflects a fit to initial performance, B is the initial estimated gain rate. For both learning functions, you can fit skill learning curves pretty well with algorithms that look for the best fit from your observed data to reasonable values of the 3 parameters.
One challenge is that data are noisy and both curve forms are pretty good at fitting pretty much any initial learning curve (that is negatively accelerated, that is, you get less improvement per time of practice as you get more practice). They start to separate at very high levels of practice, partly because the power law curve doesn’t have an asymptote. It just keeps getting better forever. That makes the curious prediction that you can always keep getting better with more practice — but is this true? Doesn’t there have to be a physical limit to the rate your muscles can contract and relax?
Which brings us back to cigars. In that 1959 study, some of the experts had been doing cigar rolling daily for more than 7 years, rolling more than 10 million cigars — and they were still learning, they were still making incremental gains. I’ve heard that there was some evidence of an asymptote (floor) in gains, but it turned out to be a function of the machine, not the ability of learning in the expert users.
There’s a good paper, Heathcote, Brown & Mewhort (2000), that argues for exponential learning curves over power-law learning curves. There’s a wee bit of math involved, but I think I’ll make decoding this kind of analysis a focus of the math/computation grad seminar this Spring. Not everybody loves papers with formulas, greek letters and calculus, but always remember: Math is Your Friend.
Update: Cigar figure